Mapping diamond surfaces using interference

This page represents a ongoing project dealing with using interference patterns to map the surface of a diamond wafer. Since this is my first page, you'll have to excuse any blatant errors that I do not pick up on immediately. Currently this page will represent my work with Dr. Richard Jones on an model of the beam splitter featured in the Michelson interferometer. I will start by giving a brief introduction to electromagnetic radiation, then move on to the model itself (including graphs,etc.).

INTERFERENCE AND LIGHT WAVES

Light (electromagnetic radiation)

An Electromagnetic Wave! (courtesy of [1])

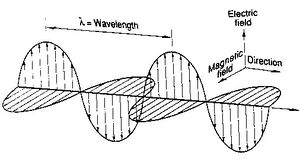
is comprised of an temporally and spatially oscillating electric and magnetic field components. These components are orthogonal to each other as well as to the direction of propagation given by the Poynting vector. Wave equations for the electric and magnetic fields can be derived using Maxwell's Equations.

$\nabla ^{2}{\boldsymbol {E}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}{\boldsymbol {E}}}{\partial t^{2}}}$

(1)

$\nabla ^{2}{\boldsymbol {B}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}{\boldsymbol {B}}}{\partial t^{2}}}$

(2)

The light waves that we used in our model of the Michelson interferometer are what are called plane waves. Plane waves are waves that have planes of constant phase, which are orthogonal to the wave vector k. Mathematically, plane waves look as follows:

${\boldsymbol {E}}={\boldsymbol {E_{0}}}e^{i\left({\boldsymbol {k\cdot x}}-\omega t\right)}$

(3)

Electromagnetic waves also have the property that they superimpose.

Interference from a Michelson Interferometer (courtesy of [2])

Like mechanical waves, EM waves can interfere destructively or constructively, but, unlike mechanical waves, there is an additional condition for light wave interference. In order for this to occur, the light waves must be traveling in the same direction, be of the same wavelength and have a constant phase with respect to each other. The reason that light waves must be travelling in the same direction to interfere is that in order for interference to occur, both the electric and magnetic field components must "line up". A picture of EM wave interference is shown at right.

INTERFEREOMETRY AND THE MICHELSON INTERFEROMETER

Interferometry is the splitting of light beams into two or more paths and the recombining of those different beams to measure difference in optical path length and refractive index [1] via interference fringes that form as a result of the recombined beams.

The Michelson interferometer

A Michelson Interferometer! (courtesy of [3])

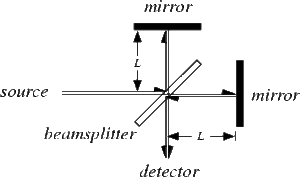
was invented by Albert Michelson in 1882 “to detect a change in the velocity of light due to the motion of the [ether]” [2]. The findings of Michelson's experiment eventually went on to support Einstein's theory of relativity.

The Michelson interferometer consists of a source, a beam splitter, a reference mirror, a target and a detector (see schematic at right). Light leaves the source and moves towards the beam splitter. The beam splitter allows half of the incident light to be transmitted and the other half to be reflected. The reflected light travels a known distance to the reference mirror, while the transmitted light travels towards the target. Both beams reflect off of their respective targets and travel back towards the beam splitter, where a similar half-half selection process occurs again. Only this time, the beams that travel back to the source are removed through an optical device, and the beams that travel to the detector "survive".

For our experiment we will be utilizing the fringes of the Michelson interferometer to gather information about the topology of synthetic diamond wafers. In order to be able to utilize a computer program to analyze the data gathered from the Michelson interferometer, we start with an model of the beam splitter present at the center of the interferometer. We know that the beam splitter is comprised of a thin layer of a conducting substance present on one side of a thin piece of optical glass. When a beam of light is incident on the beam splitter, a fraction of the photons travel through to the other side of the splitter and the remaining photons reflected. Here we consider wavelengths at which the fraction of the beam absorbed by the mirror is negligible.

Using our knowledge of electric and magnetic fields in conductors and Maxwell's Equations, we can create a simple model of the beam splitter with a light wave at normal incidence. We are interested in finding two main quantities in this model: the thickness of the conducting film and the phase shift that occurs at the mirror surface.

Using the programming power of Matlab, we can solve our system of equations Mv=b, where M, v, and b are given below.

$M={\begin{bmatrix}-1&1&1&0\\Z_{1}^{-1}&Z_{2}^{-1}&-Z_{2}^{-1}&0\\0&e^{ik_{2}a}&e^{-ik_{2}a}&-e^{-ik_{1}a}\\0&Z_{2}^{-1}e^{ik_{2}a}&Z_{2}^{-1}e^{-ik_{2}a}&-Z_{1}^{-1}e^{-ik_{1}a}\end{bmatrix}}$

(4)

$v={\begin{bmatrix}E_{r}\\E_{f}\\E_{b}\\E_{t}\end{bmatrix}}$

(5)

$b={\begin{bmatrix}1\\Z_{1}^{-1}\\0\\0\end{bmatrix}}$

(6)

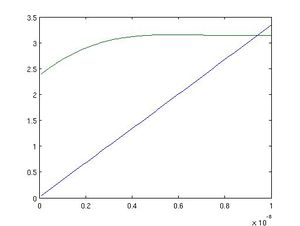
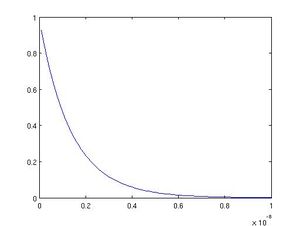
Using Matlab we were able to extract information about the desired depth of the conducting film and the phase shift that occurred when the light wave traveled through the the film. Our graphs dislpaying phase shift versus depth and amplitude versus depth are shown below.

A Graph of the Phase shift versus Thickness

A Graph of Amplitude versus Thickness

Maxwell's Equations

References

1. C. Candler, Modern Interferometers, Hilger & Watts Ltd., 1951, p.9.

2. ibid, p.110.