Characterizing SiPMs

SiPM Performance Requirements

The tagger microscope consists of many identical and well isolated readout channels, each consisting of a several cm long scintillating fiber connected to a clear acrylic fiber light guide. A tagging electron travels axially down the length of a scintillating fiber depositing 4 MeV of energy in the fiber, resulting in 1600 scintillation photons within the forward capture cone of the fiber. Assuming that 80% of these are delivered to the SiPM active surface and a conservative estimate of 15% for the efficiency of the SiPM leads to an estimate of 190 for the average SiPM pixel count per event. Monte Carlo simulations have shown that an efficient detection threshold corresponds to 40% of the average pulse height, or 80 SiPM pixels. This implies a requirement for the dark rate that spontaneous pulses never exceed 80 pixels.

The large photon yield expected at the end of the light guide does not demand unusual detection efficiency on the part of the SiPM. For example, 10% efficiency with the above number of photons still yields a signal of 130 photons. However, given that the scintillator (BCF-20) has a finite decay time (2.7ns) the more photons are produced the more clearly resolved is the time of the pulse.

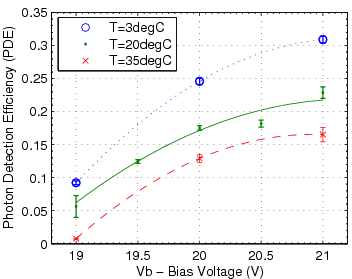
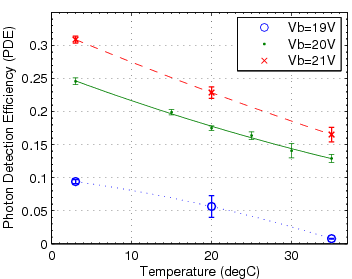
The device is expected to have a high enough gain (measured in electrons per photon detected) - around 10⁶. in order for such a small light signal to be recorded by conventional electronics. Such devices are also susceptible to spurious, thermally excited pixel breakdowns, each showing up as a single photon hit ("dark count"). High rate of these single-pixel events may create a pileup above the signal threshold. All of the above parameters (detection efficiency, gain and "dark rate") depend on applied bias voltage and temperature. Stability of performance despite expected fluctuations of these variables is an important requirement.

Another criterion in SiPM selection is its dynamic range. Although this readout device essentially provides digital output - scintillation detected or not - enough of a range is necessary to set a threshold above the noise floor and to account for some pixels being not having required from a previous hit .

Bench Test Setup

Hardware

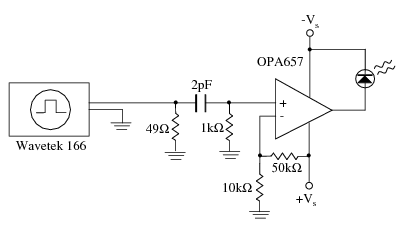
A pulser circuit designed to drive the LED for photo-detector bench tests. The circuit differentiates the input signal, thus the amplitude of the input square wave controls pulse amplitude up to the saturation point, at which the pulse shape broadens to a maximum of 6 ns. V_s = 5 V

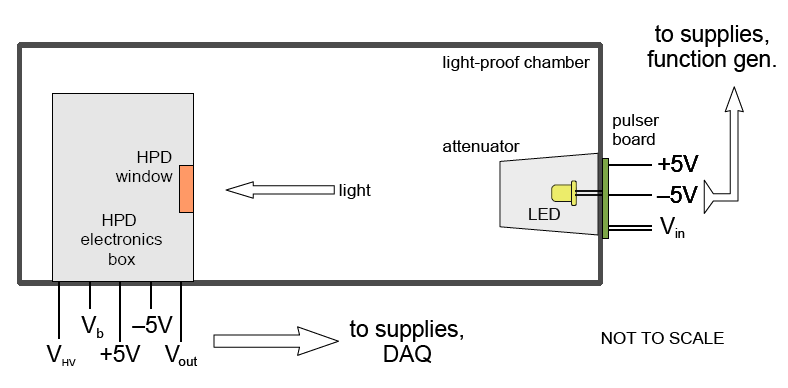
A wooden dark box was initially constructed for the a hybrid photo-diode (HPD) module DEP PP0350. A pulser was installed on the opposite end of the box composed of a fast LED driven by a pulser circuit shown on the right.

Running this setup with an HPD of known characteristics allows us to calibrate the light intensity. The SiPM detection efficiency can then be characterized relative to the HPD. The signal from the SiPM was clean enough to distinguish peaks corresponding to discreet photon (pixel) counts in the histogram signal integrals. Therefore, the gain of the SiPM was found independently of the HPD - the SiPMs were self-calibrating! The measurements section below describes this feature further.

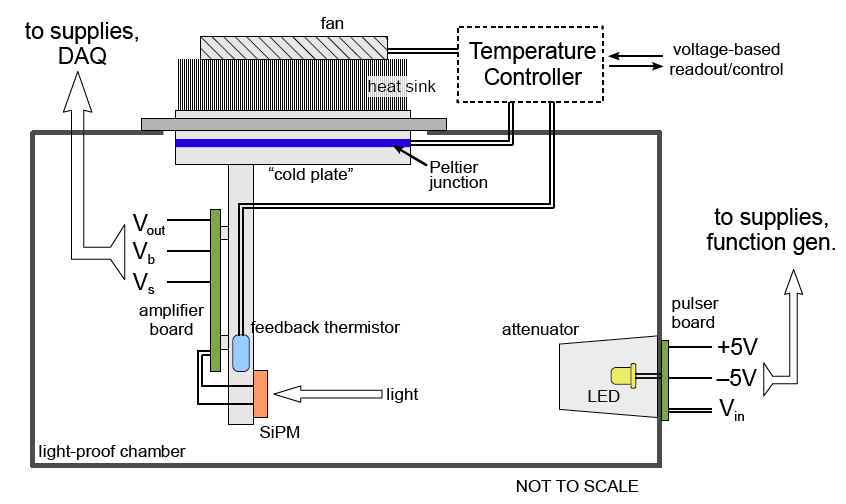
Below are the diagrams of the dark box with the HPD and SiPM assemblies installed. A temperature controller system (TE Tech. TC-24-12) was procured, which operates by driving a Peltier junction based on feedback from a thermistor compared to voltage-specified reference temperature. It was calibrated and installed into the wall of the dark box via a custom-designed light-tight frame.

Diagram of the dark box with the HPD module installed. V_HV = -12 kV, V_b = 60 V.

Diagram of the dark box with a SiPM mounted on a temperature-controlled cold plate. V_b is the bias voltage discussed below, V_s is the preamplifier supply voltage set to 5 V in our work (recommended levels: 4 - 9 V)]]

Data Acquisition

A Tektronix TDS 2024 (2Gsmp/s, 200MHz) is used to acquire the SiPM signal from its preamplifier, the response of which is well understood based on detailed analysis and simulation. Since tens of thousands of waveforms are necessary to construct a clean histogram of collected charge, a fast PC based data collection system was necessary. The data export module installed on this oscilloscope allows RS-232 interface over which commands can be issued and data transfer requested. Unfortunately going above the baud rate of 9600 always resulted in lost bytes. At 9600 the 2500-sample waveform collected by the oscilloscope takes about 2-3 seconds to transfer. Since we are dealing with time windows of 1μs in which the unit is too slow to collect all 2500 samples (it was found to copy or interpolate between actual samples) it was resolved to just collect the first 1000 samples, corresponding to the first 4 divisions on the screen. The waveforms now trickled at one per second.

For the purposes of collecting integrals of waveforms (proportional to total charge collected per received flash) it was later found that the averages of the functions can be requested much faster, about 3 per second. This value times the window duration equals the desired integral!

Aside from the convenience of usable results within hours instead of a day, is the issue of avoiding systematic drifts. It was found that while higher statistics smooth out the histogram of integrals, there are also drifts, whether due to environmental variations over the course of a day or electronic effects. These drifts smeared the histograms, most of which already had a very faint sign of photon peaks. So, faster data acquisition also meant avoiding these drifts.

SiPM Measurements

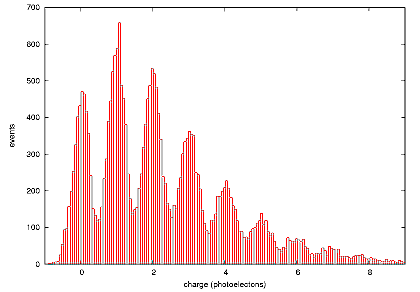
Illustration of discrete peaks seen in the collected SiPM charge frequency histogram. The first peak shows the number of events in which no photons were detected, the next shows one and so forth. Note the even spacing of the peaks, showing the linearity of the device.

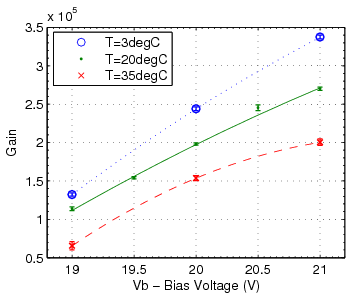
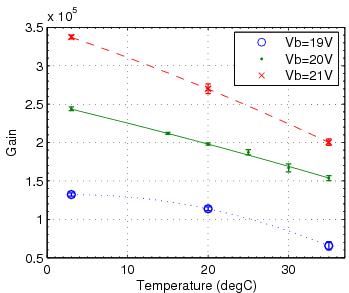
The first remarkable feature of the the SiPM statistics is the presence of discrete peaks in the histogram of charge collected in the SiPM(proportional to the SiPM signal (V) integral (Vs) by 1/Gain_{trans-impedance} (A/V). This allows us to determine the charge collected per activated pixel (per photon) and therefore gives the gain of the device. This is the "self-calibration" referred to above.

The general analysis procedure was to

histogram the collected set of function integrals
get the pedestal: the first peak corresponds to events with no photon hits, so it properly belongs at zero [charge collected]
gain is calculated and histogram rescaled: the width between adjacent peaks corresponds to the the gain in units of Vs/pixel. (Using the amplifier trans-impedance gain value, this can later be converted to charge/pixel)
mean of this shifted, rescaled set is calculated. Since each peak is now pegged to photon count, the mean is in the units of average photons received. Based on this value, corrected by the dark count (described below), the efficiency of the SiPM can be calculated by comparing this average flux to that felt by the HPD.

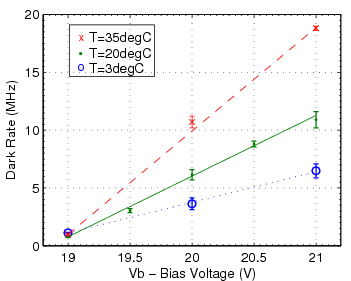
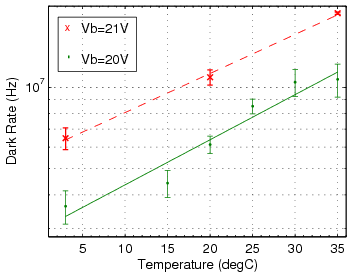
This procedure is repeated with the LED and/or SiPM covered to measure the dark rate. Depending on which distribution showed the photon peaks more distinctly, either the illuminated or dark datasets were used for the gain calculation and pedestal calculation. Either way, a mean was extracted from the dark distribution to calculate the dark rate and to subtract the average dark pixel count measured from the average pixel count measured while illuminated.

Below is the summary of results obtained from these measurements performed on the two SiPMs acquired from Photonique.

Summary of SiPM Properties measured at room temperature at recommended bias voltages
Device	Gain		PDE (yellow)		Dark Rate
Device	Nom.	Meas.	Nom.	Meas.	Nom.	Meas.
SSPM-050701GR-TO18 [1]	0.8×10⁶	1.1×10⁶	~29%	~30%	10 MHz	9.8 MHz
SSPM-0606BG4-PCB [2]	1.5×10⁵	2.5×10⁵	27%	20-23%	15 MHz	8.9 MHz


Dark rate plotted as a function of bias voltage at extreme and room temperatures and as a function of temperature at different bias voltages. Note the disappearance of temperature dependence at low bias voltage.


SiPM gain plotted as a function of bias voltage at extreme and room temperatures and as a function of temperature at different bias voltages.


Photon detection efficiency as a function of bias voltage at extreme and room temperatures and as a function of temperature at different bias voltages.